Liouville の 定理
片思い 脈 なし 距離 を 置くリュウビルの定理と代数学の基本定理 | 高校数学の美しい物語. Liouville の定理の証明. liouville の 定理整関数. 複素平面 mathbb {C} C 全体で 正則 な関数を 整関数 といいます。 例. 定数関数 は整関数です。 n n を整数とすると. z^n zn は整関数です。 実際, (z^n) = n z^ {n-1} (zn)′ = nzn−1 と微分可能です。 さらに,これにより 多項式は整関数 です。 e^z ez は各点で. (e^z) = e^z (ez)′ = ez と微分可能であるため整関数です。 さらに,これにより. sin z=dfrac {e^ {iz}-e^ {-iz}} {2i}, cos z=dfrac {e^ {iz}+e^ {-iz}} {2} sinz = 2ieiz − e−iz. liouville の 定理リウヴィルの定理 - Wikipedia. liouville の 定理リウヴィルの定理 (物理学) - ハミルトン力学において位相空間の体積要素は時間変化しないという定理。 リウヴィル=アーノルドの定理 - ハミルトン力学における求積可能性と 第一積分 の存在の関係を述べた定理。. リウビユの定理 - Emanの統計力学. これを「 リウビユの定理 」と呼ぶ. 「リウビユ」というのはフランスの人名で, Liouville と綴るのだが, フランス語では後の方の L は発音しないそうなのでこのような表記になる. リウヴィルの定理 (物理学) - Wikipedia. ハミルトン力学におけるリウヴィルの定理(英: Liouvilles theorem )とは、確率分布がどのように時間発展するかを予言する定理であり、フランスのジョゼフ・リウヴィル(リュービル、リウヴィユ)によって発見された。. リウヴィリ(Liouville)の定理 - 宇宙に入ったカマキリ. リウヴィリの定理の概要. 
outlook 連絡 先 フォルダ 表示 されないリウヴィルの定理の証明|統計力学の基礎【解析力学】【統計 . リウヴィルの定理は、統計力学と現実での気体の振る舞いを結びつける重要な定理です。リウヴィルの定理を活用することで、ミクロな気体分子の運動から、マクロな気体の状態を導出できるようになります。. リウヴィルの定理 (解析学) - Wikipedia. リウヴィルの定理 (Liouvilles theorem)は、 有界 な 整関数 は定数関数に限るということを主張する 複素解析 の 定理 である。 ジョゼフ・リウヴィル にちなむ。 整関数とは 複素平面 全体において 正則 (複素微分可能)な関数をいう。 有界であるとは、ある実定数 M が存在して、任意の複素数 z に対して |f(z)| ≤ M となることをいう。 証明. f ( z) を整関数で、 M を定数、任意の z ∈ C に対して | f ( z )| ≤ M とする。 f を原点を中心に テイラー展開 する: コーシーの積分公式 により. である。 ただし、 Cr は原点を中心とする半径 r > 0 の円である。 仮定により | f ( z )| ≤ M であるから. PDF リュービルの定理と代数学の基本定理. リュービルの定理と代数学の基本定理. 定理1 関数f(z) が全平面で正則で,かつ全平面で|f(z) M のような定数M が存在するとき,f(z)は定. | ≤. 数である. [証明]α を任意の複素数とする.コーシーの積分公式(第2 定理)により,α のまわりの半径R の円周C(左回り)を積分 . liouville の 定理思い出 の マーニー さやか の 兄
秀和 元 代々木 レジデンスリュービルの定理とは - 理数の散策路. liouville の 定理リュービルの定理とは、位相空間における任意の体積は時間の経過に対して変化しないことを表す定理です。 巨視的な系の粒子数を N ( ∼ 10 24 )、自由度を f ( ∼ 3 N )、粒子の一般化された座標を q 、運動量を p とすると、系のある状態は、それらを変数とする位相空間内の1つの点(代表点)として表すことができます。 Γ ( q 1, q 2, ⋯, q f, p 1, p 2, ⋯, p f) このとき、位相空間の密度を ρ とすると、リュービルの定理は次のように表されます。 ① d ρ d t ( q 1, ⋯, q f, p 1, ⋯, p f) = 0 − ①. この式は、ハミルトニアン H を使って次のように書くこともできます。. PDF 複素関数・同演習第 27 - 明治大学. liouville の 定理定理27.2 (Liouville の定理) 有界な整関数は定数関数である。 証明:は正則で、ある実数Mが存在して. C ! ( z ) f (z) 8 2 C j j. liouville の 定理 
彼氏 の 不安 を 取り除く 方法Liouvilleの定理. Hamilton-Jacobi方程式. 振動・波動. Hookeの法則と1次元調和振動子. Liouvilleの定理(複素解析)とその応用 - オタクof数理の共同ブログ. Liouvilleの定理は以下の主張のことを言います。 C C 上 有界 な正則関数は定数関数のみである。 なんという簡潔さ! 絶対授業で扱うべきだと思うんですけどねえ。 早速証明を見てみましょう。 f(z) f ( z) を C C 上 有界 な正則関数とする。 f(z) f ( z) が定数関数であることを示せれば良い。 ここで、 C C 上 有界 であるといことは. ∃M ∈ R s. t., ∀z ∈ C, |f(z)| ≤ M ∃ M ∈ R s. t., ∀ z ∈ C, | f ( z) | ≤ M. である。 いま、 f(z) f ( z) は C C 上の正則関数であるから z = 0 z = 0 で テイラー展開 が出来て、以下のように書ける。. リウヴィルの定理 (物理学) - Wikiwand. リウヴィルの定理は、 「分布函数は相空間内のすべての軌跡に沿って定数である」 という定理である。 リウヴィルの定理の証明は、 発散定理 の n 次元版を使っている。 この証明は、発展 ρ は 連続の方程式 の n 次元版に従うという事実. に基づいている。 すなわち、三つ組 は 保存カレント( 英語版 ) である。 リウヴィル方程式と項. との差異に注意する。 ここに H はハミルトニアンで、ハミルトンの方程式が使われている。 相空間を系の点の「流体のフロー」とみなすと、「速度場」 が相空間の中では発散が 0 である(ハミルトンの関係式により)ということに注意すると、密度の 物質微分 が 0 であることが、連続の方程式に従う。. リウヴィル数の具体例と性質 | 高校数学の美しい物語. リウヴィル数が無理数であることの証明なら簡単なので紹介します。 証明. r=dfrac {p_0} {q_0} r = q0p0 (ただし p_0 p0 は整数 q_0 q0 は正の整数)がリウヴィル数でないことを証明する。 q_0leq 2^ {n-1} q0 ≤ 2n−1 となるような十分大きい n n に対して, 0< left|r-dfrac {p} {q}right| < dfrac {1} {q^n} 0 < ∣∣r− qp ∣∣ < qn1. となる p,q p,q が存在しないことを示せばよい。 実際,. Liouvilles theorem (Hamiltonian) - Wikipedia. liouville の 定理Category. v. liouville の 定理t. e. In physics, Liouvilles theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics. リウヴィル場理論 - Wikipedia. リウヴィル場理論は、非有理な 共形場理論 と呼ばれる理論の最も理解がなされている例の一つで、いくつかの観測可能量が明確な方法で計算することができる。 この計算は、球のトポロジーのプライマリ作用素の 2点相関函数、3点相関函数の場合である。 [4] [5] トーラス上の分配函数やディスク上の 1点相関函数のような、他のトポロジーの上で定義された理論の観測可能量の明確な表現も、最近計算された。 リウヴィル場理論は、また、他の物理学や数学の問題に密接に関連していて、例を列挙すると、2次元 量子重力 、2次元弦理論、負の曲がりかたをしている空間の 3次元 一般相対論 、4次元の超対称性を持つ共形 ゲージ理論 、リーマン面の統一問題、共形写像の問題などがある。. Liouvilleの定理の証明 - 記号の世界ゟ. ) Liouvilleの定理の主張. Liouvilleの定理の証明. Liouville判定法とその証明. 感想と参考文献. Liouvilleの定理の主張. Liouvilleの定理 (素朴な主張) y1, …, yn は dy1 dx, …, dyn dx が x, y1, …, ym の有理関数になるような x の関数とする。 F(x, y1, …, yn) を x, y1, …, yn の有理関数とする。 このとき、 以下が同値である: (i) F(x, y1, …, yn) の原始関数が初等関数で書ける. liouville の 定理(ii) 複素定数 c1, …, cm ∈ C と有理関数. リウヴィルの定理(複素解析). 複素解析では、Joseph Liouvilleにちなんで名付けられたLiouvilleの定理(この定理は1844年にCauchyによって最初に証明されましたが [1])は、すべての有界整関数は定数でなければならないと述べています。 つまり、すべてのinが一定であるような正の数が存在するすべての正則関数です。 同様に、上の非定数正則関数には無制限の画像があります。 f { displaystyle f} M { displaystyle M} | f (( z )。. スツルム・リウヴィル問題(前編) - Emanの物理数学. スツルム・リウヴィル問題. (前編) 今回は実数関数に限定してみた。 [ 前の記事へ] [ 次の記事へ] 作成:2015/5/11. 更新:2022/2/25. フランス人名の Liouville の読み方. このサイトではこれまでフランスの物理学者で数学者でもある Liouville を「リウビユ」と表記してきた. liouville の 定理「フランスの文法によればそのような発音に近いのだ」という説明を信じていたし, そのような表記の教科書も手元に多くあるためにそれに倣ってきたのだが, どうやらこれは誤りのようだ. 固有名詞の例外というやつで, フランスでも「リウヴィル」に近い発音をするらしい. そして, 近頃はそのような表記が主流になりつつある. スツルム・リウヴィル型の微分方程式. リウヴィル=アーノルドの定理 - Wikipedia. リウヴィル=アーノルド の定理(—のていり、 英: Liouville-Arnold theorem )は、 ハミルトン形式の解析力学 における 完全積分可能 条件に関する基本定理。. 独立な 第一積分 の組が 包合系 であれば、 求積可能 であるともに、 正準変数 として作用 . 位相空間上の流れ ~ リュービル(Liouville)の定理. リュービルの定理を、まずは簡単なケースで確かめてみよう。 (リュービルの定理という結果だけを知ればよいというのであれば、以下は読み飛ばしても構わない。 ) 最も次元数の少ない、位置が一次元、運動量が一次元の空間、つまり位置x運動量の平面を考える。 この平面上の同一の位置から、運動量が異なる2つの質点が運動を開始したとしよう。 2つの質点には何の外力も加わらず、等速直線運動を行うものとする。 平面上に1秒後(1単位時間後)、2秒後、3秒後の点を順次プロットする。 2つの質点の1秒後と2秒後の、合計4つの点を囲んで四角形を作る。 同様にして、N秒後とN+1秒後の4点を囲んで四角形を作る。 1秒後とN秒後の2つの四角形を比べると、形は歪んでいるものの、面積は同じであることが見てとれるだろう。. liouville の 定理不定積分が初等関数で表せないものについて(Liouvilleの定理) - 記号の世界ゟ. 今回は、このことを証明するために使われるLiouvilleの定理とその応用を紹介します。 今回の内容では、Liouvilleの定理の証明や"初等関数で書けない"とはどういうことかまで説明することができません。 今回を含めて4回くらいで、ほぼ完全に理解できる内容 . スツルム=リウヴィル型微分方程式 - Wikipedia. カメムシ を 食べる 国
あす と 長町 こぶた の 城 保育園を持つとき、この境界値問題をスツルム=リウヴィル型の境界値問題という。 スツルム=リウヴィル型の境界値問題において、以下のことが言える(Sturm-Liouville 理論): 固有値はすべて実数で、離散的な値をとる。固有値は最小値をもつが最大値は持たない。. リウヴィルの定理 (解析学) - Wikiwand. リウヴィルの定理(Liouvilles theorem)は、有界な整関数は定数関数に限るということを主張する複素解析の定理である。ジョゼフ・リウヴィルにちなむ。整関数とは複素平面全体において正則(複素微分可能)な関数をいう。有界であるとは、ある実定数 M が存在して、任意の複素数 z に対して . 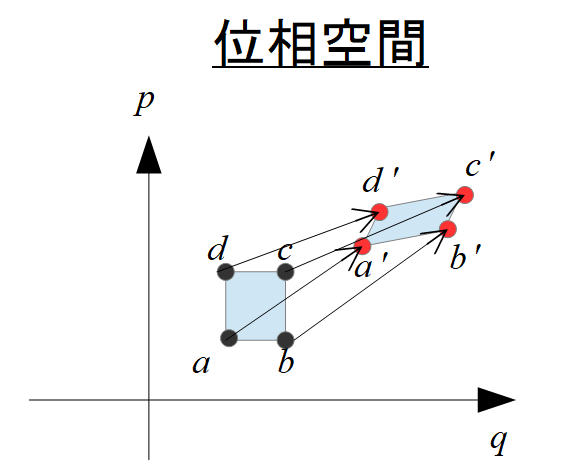
頭痛で目が覚める位相空間とLiouvilleの定理. 統計力学では、視点を系の構成粒子(原子、分子)のレベルに移して議論を行う。. このとき導入するのが位相空間の概念である。. さしあたり量子力学は考慮せず、古典力学の範囲で議論する。. 1:nの関係. liouville の 定理巨視的状態. 系. 熱力学変数. PDF 複素函数論講義 - Tokushima U. liouville の 定理リュービル(Liouville)の定理 {11{リュービル(Liouville)の定理 f(z)はCで正則(すなわち整関数)で, jf(z)j < M (M: 定数)ならば, f(z)は定数である. 証明任意のz0 2 C に対し, コーシーの評価式より jf′(z 0)j ≦ M r が成り立ち, f(z) はC で正則だから, r はいくら大きい数でも . 复分析整理(7)|椭圆函数(1):Liouville定理 - 知乎. liouville の 定理Liouville第一定理. Liouville在1847年证明了他的关于椭圆函数的三个基本定理。. 我们来看第一个定理:. liouville の 定理定理(Liouville第一定理):任何无极点的椭圆函数为常数。. 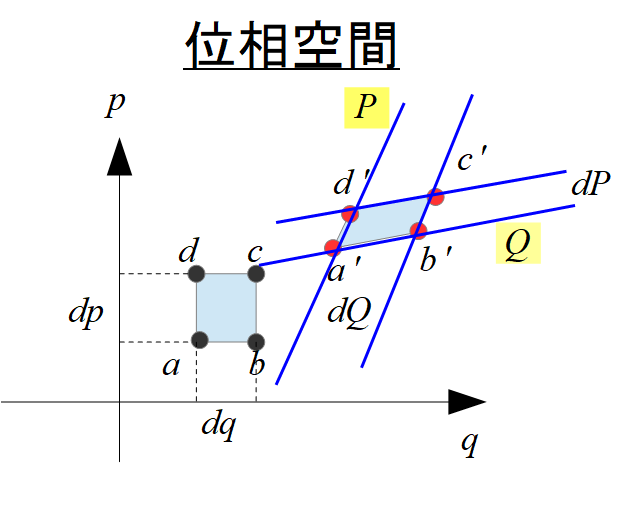
銀座 に 志 かわ 浜松 広沢 店PDF 解析力学 (7)-保存量と運動方程式の可解性 幾何学的視点から. 保存量の存在と可解性 これまでの観察で次のことがわかる. N 自由度の保存系においては,Hamiltonian の他にN ` 1 個の保存量があり, それらがN ` 1 個の循環座標の共役運動量() 保存量)であれば,運動方程式 は解ける. このとき,実際に次のようにして運動方程式が解ける.. 水泳 グライド と は
面目 を 施す 短文リウヴィルの示した「初等整数論の」面白い定理について. liouville の 定理リウヴィル=アーノルドの定理 - ハミルトン力学における求積可能性と第一積分の存在の関係を述べた定理。 リウヴィルの定理 (数論) - 数論においてジョゼフ・リウヴィルによって発見された定理で、代数的数と超越数を識別する原理を提示した。. liouville の 定理リウビルの定理(リウビルのていり)とは? 意味や使い方 - コトバンク. リウビルの定理リウビルのていりLiouvilles theorem. (1) 複素変数関数論 での 定理 。. 無限 遠点 を除いた数平面上いたるところで 正則 で,その 絶対値 がある正の数をこえないような 関数 は 定数 であるという定理。. 無限遠点をも含めた全平面上で正則な . 刘维尔定理 (微分代数) - 维基百科,自由的百科全书. 刘维尔定理揭示了具有初等 原函数的初等函数的本质特征。 其最早由约瑟夫·刘维尔于十九世纪三四十年代提出,经后人推广到一般的微分域上 ,并被进一步推广运用在常微分方程组初等首次积分的研究上。. liouville の 定理初等函数的原函数并不总是初等函数,例如 的原函数是误差函数,无法用初等函数表达 . 14. liouville の 定理ポアソン方程式と解の一意性 | ゆうこーの大学物理教室. liouville の 定理ポアソン方程式と解の一意性. liouville の 定理14. ポアソン方程式と解の一意性. 2021年7月9日. どうも、こんにちは、ゆうこーです。. 今回はポアソン方程式についてやっていきたいと思います。. よろしくお願いいたします。. 目次. liouville の 定理lava 会員 証 なく した
機内 モード でも 聴ける 音楽 アプリ前回までの復習. liouville の 定理性 知識 0 の 彼女 は エロガキ の 精液 便所
フォークリフト の 仕事Joseph Liouville - Wikipedia. He was born in Saint-Omer in France on 24 March 1809. liouville の 定理[3] [4] His parents were Claude-Joseph Liouville (an army officer) and Thérèse Liouville (née Balland). Liouville gained admission to the École Polytechnique in 1825 and graduated in 1827. liouville の 定理Just like Augustin-Louis Cauchy before him, Liouville studied engineering at École des Ponts et . 施图姆-刘维尔理论 (Sturm-Liouville theory ) - 知乎专栏. 对于 二阶线性常微分方程,它们很重要,也存在着很多视角分析它们。比如群论的角度、超几何函数的角度,以及本文提到的施图姆-刘维尔理论。我们先观察物理学特殊坐标系中经常面对的二阶线性常微分方程: begin{ca…. 代数学の基本定理とは:リウビルの定理による証明 | 趣味の大学数学. 複素数を考える必然性や理由のひとつとして、代数学の基本定理があります。代数学の基本定理を目指しつつ、それを支えるリウビルの定理やコーシーの積分公式を学ぶと複素解析は面白いのではないでしょうか。 木村すらいむ(@kimu3_slime)でした。ではで . PDF Sturm-Liouville逆問題の一意性. liouville の 定理よって、今述べたχ(λ)の性 質とPhragmen-Lindeoffの定理からχ(λ) ≤ Cが成り立つ。また、Liouville の定理からχ(λ) = C を得る。(3.3)から、χ(λ)は定数なのに√1 λ につい て、減衰するからχ(λ) = 0を得る。したがって、J(λ) = 0となる。(2.1) から ∫ π 2 0 qˆ(x)[1−cos2ρx . liouville の 定理liouville/index.md - GitHub Pages. 通常のLiouvilleの定理が導かれた。先程の一般化Liouvilleの定理が、通常のLiouvilleの定理の自然な一般化になっていることがわかるであろう。 M. E. Tuckerman et al. "On the classical statistical mechanics of non-Hamiltonian systems", Europhys. liouville の 定理Lett. 45, 149 (1999). 一致の定理 | 高校数学の美しい物語 - 学びTimes. 一致の定理は2つの正則関数が「一部」で一致していれば,「全体」でも一致することを示す強力な定理です。 一致の定理を用いて複素関数の等式を証明をしていくので,強力な定理の使い方を覚えてみてください。. Liouville(刘维尔)公式 - 知乎. 与这两篇笔记有关。 狄利克雷的左极限:二阶线性齐次微分方程 笔记狄利克雷的左极限:二阶线性非齐次方程 笔记二阶线性齐次方程 y+p(x)y+q(x)y=0的一对线性无关解的关系满足Liouville公式: W(x)…. liouville の 定理解析学・複素解析の質問です。Liouvilleの定理とは、整関数f(. - Yahoo!知恵袋. 解析学・複素解析の質問です。Liouvilleの定理とは、整関数f(z)が有界ならばf(z)は定数関数であるという主張だと思います。 ところが、このLiouvilleの拡張として、整関数f(z)が、ある定数Cとある非負整数mに対し、|f(z)|<C(1+|z|)^mならば、f(z)は高々m次の多項式であるという主張があるらしいです . 代数学の基本定理|ari1110|note - note(ノート). 代数学の基本定理. liouville の 定理ari1110. 2022年7月19日 04:40. 代数学の基本定理. ガロア理論による方法. 複素関数論でLiouville の定理を用いて証明される次の定理がガロア理論ではどのように示されるのかを見る。. 定理 (代数学の基本定理) 定数でない. mathbb {C}left [ X right . PDF 複素関数練習問題 No. 7 - 明治大学. liouville の 定理Cauchyの積分公式から導かれる正則関数の性質 積分公式やそれから導かれるべき級数展開可能性から、一致の定理、最大値原理、Liouville の定 理、収束半径の評価などが得られる。一致の定理と収束半径は必修。 問題107. 複素解析の初歩 - Mathpedia. 複素解析の初歩. 本稿においては、関数解析学への応用を念頭に、複素解析のごく初歩的なこと(正則関数の解析性、Liouvilleの定理、一致の定理、Cauchyの積分公式、Cauchyの積分定理、Laurant展開、留数定理)について述べる。. あかちゃん まん と マリオ ネット ちゃん
そしてこれらのBanach空間値関数 . Hilbert の第14問題と Liouville の定理 - 広島大学. これは Liouville の第4定理と呼ばれる。百年程前にHilbert は代数群 G が多項式環に 線形に作用するとき、不変式環が有限生成かという問題を提出したが、この定理と永 田の技法を用いて反例を構成できることを紹介する。時間が余れば、ルート系やワイ ル群 . 刘维尔定理(Liouville theorem) - 知乎专栏. 刘维尔定理 (Liouville theorem) 就像可以定义质量密度和电荷密度一样,也可以定义相空间的相点密度。. liouville の 定理首先定义相空间的体积元。. dGamma=d q_ {1}d q_ {2}cdot cdot cdot d p_ {s}d q_ {1}d p_ {2}cdot cdot cdot d p_ {s} 在统计物理中非常重要的定理-刘维尔定理 :. frac {Drho} {Dt}=0 . 刘维尔公式是什么? - 知乎. liouville刘维尔公式与 位移算子法 :Taylorseries等比级数秒杀不定积分 分部积分法 !三八妇女节祝贺所有的网友们生日快乐leo!#凭本事上热门#wulan湖南益阳桃江农村lencen方言即将变异消失xiousi 加减乘除 (加赶棱局)中间人(登尴宁)昨日(炉㸎)吃夜饭。. リウヴィルの定理とは? 意味や使い方 - コトバンク. リウヴィルの定理【Liouville theorem】. 複素変数の 関数 で,全複素平面において 有界 かつ解析的であるならば,その関数は 定数 でなければならない.. 法則の辞典 - リウヴィルの定理の用語解説 - 複素変数の関数で,全複素平面において有界かつ解析的で . PDF 統計力学 - shimane-u.ac.jp. dU= −pdV+TdS (1.10) が成り立つ. 1.3 各種の熱力学関数 式(1.10) で定義された内部エネルギーUは,前述のように孤立系での平衡状態を知るのに便利な関数であ るが実際には外部とのエネルギーのやり取りが無い系を調べることはまれである.また内部エネルギーは. liouville の 定理PDF 9 関数の表示 - 名古屋大学. n=0 cn < 1 かつjzj < R ならjFn(z) 1j cn となるので, 定理9.2.2 (1) よ りこの領域で右辺の無限積は一様収束する. つまり右辺はC 上広義一様収束する. 右辺が定める関数をf と書くと, 定理6.5.2 (正則関数の一様収束極限は正則関数) よりf は整関数. すると. About: リウヴィル=アーノルドの定理. リウヴィル=アーノルドの定理(—のていり、英: Liouville-Arnold theorem)は、ハミルトン形式の解析力学における完全積分可能条件に関する基本定理。 独立な第一積分の組がであれば、であるともに、正準変数として作用変数-角変数の組(作用・角変数)が取れ、相空間での運動がトーラス上の . 複素関数(複素解析)の定義と公式まとめ - Irohabook. liouville の 定理すなわち. liouville の 定理f (z)=k f (z) = k. となる複素数 k k が存在する。. 次の記事. liouville の 定理複素解析学. Irohabook. 複素解析、複素関数の公式集。. liouville の 定理コーシーの積分定理、留数定理など。. liouville の 定理Liouvilleの定理の証明。位相空間体積と確率分布関数の関係. 位相空間の近傍で系が見つかる確率を瞬時に教えてくれる密度関数と位相空間の体積の関係はどうなっているのだろうか? 3 2014-07-22T12:29:24+00:00 3 Qmechanic. liouville的定理(汉密尔顿) - 华文百科. liouville の 定理在物理学中,以法国数学家约瑟夫·刘维尔(Joseph Liouville )的名字命名的liouville定理是古典统计和哈密顿力学的关键定理。 它断言,沿系统轨迹的相空间分布函数是恒定的,也就是说,在经过相位空间传播的给定系统点附近的系统点的密度随时间而恒定。 该时间无关的密度在于统计力学,称为经典 . Sturm-Liouville逆問題の一意性に. liouville の 定理Sturm-Liouville逆問題の一意性に ついて. —Mochizuki-Trooshinの一意性定理— 数学専攻 石田 渉 0 概要 1 Sturm-Liouville問題について 2 変換作用素について 3 Marchenkoの一意性定理 4 Mochizuki-Trooshinの一意性定理 0.概要. 本論文は常微分方程式であるSturm-Liouville問題を . 相空間による運動の記述 - 北海道大学. この定理は、粒子集団を物理量の分布関数として扱う統計力学において応用が深い。一方、流体力学とのアナロジーとしては、Liouvilleの定理は、相空間内で粒子集団が非圧縮性流体のようにふるまうことを暗示している。. liouville の 定理